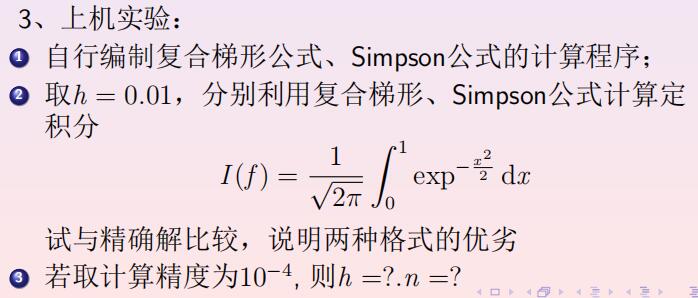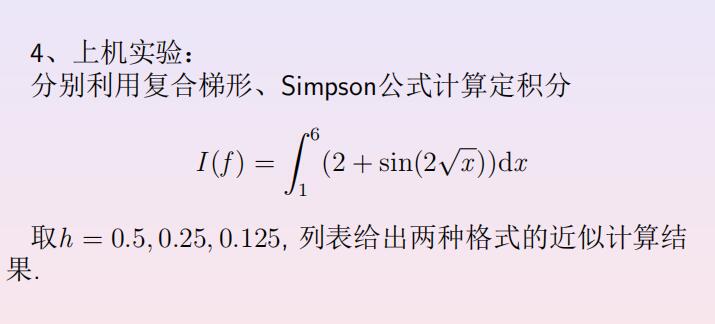[TOC]

第一章 误差理论

背景知识

描述了误差的来源于类型、度量方法、误差的收敛阶、误差的累计以及局部与整体误差。

误差的来源与类型

模型误差

我们在计算时经常将问题进行数学建模，建模往往省略了一些影响小的变量，近似地模拟了问题，我们吧数学模型与实际问题之间出现的这种误差称为模型误差。

截断误差

数学模型的数值解或者准确解有时候很难求，这时我们往往用数值方法来求他的近似解，这样产生的误差被称为截断误差，或者叫方法误差。

舍入误差

计算机字长有限不能表示出无限的数字，这时我们参与运算的时候会取近似值，比如说 $\pi$。

浮点数舍入误差

这里涉及的是计算机浮点数的表示方法。我们以双浮点数64位为例。分为三部分，第一位是符号位$s$，之后十一位是指数位$c$，剩下五十二位是尾数位$f$。可以表示为
$$(-1)^s2^{c - 1023}(1+f)$$
我们可以得到它的上限为
$$2^{2014}(2 - 2 ^ {-52})$$
下限为
$$2^{-2013}(1 + 2 ^ {-52})$$
所以更大的或者更小的是不能表示的，实际上在这之间随着数据增大或者减小，表示都是逐渐变得不准确的。

误差的度量方法

假设$p*$是$p$的近似值，我们定义以下概念：

• 绝对误差
  $$|p - p^*|$$
• 相对误差
  $$\frac{|p - p^*|}{|p|}$$

迭代法的收敛阶

设迭代过程 $x_{k+1}=\varphi (x_k)$ 收敛于方程 $x=\varphi(x)$ 的根$x^{}$，
如果迭代误差 $e_k=x_k-x^$，且$\lim_{k \to \infty}\frac{|e_{k+1}|}{|e_k|^p}=c\neq 0$成立，则称序列$\lbrace{x_k}\rbrace$收敛于$x^*$具有p阶收敛速度，简称$\lbrace{x_k}\rbrace$是p阶收敛的。常数c称为渐进收敛常数，也称为收敛因子。

1. $p = 1,0 \leq c \leq 1$时为线性收敛
2. $p > 1$称为超线性收敛
3. $p > 2$称为平方收敛

误差传播

设$p\hat{}, q\hat{}$ 为$p, q$的近似值， 误差分别为$\epsilon_p , \epsilon_q $
和运算
$$p + q = p\hat{} + q\hat{} +\epsilon_p + \epsilon_q $$
积运算
$$pq = p\hat{} q\hat{} + p\hat{} \epsilon_q + q\hat{} \epsilon_p + \epsilon_p \epsilon_q$$

实验

问题

1. 求方程$x^2 + (\alpha + \beta)x + 10^9 = 0 $的根，其中$\alpha = -10^9 \beta = -1$, 讨论如何设计计算格式才能有效地减少误差，提高计算精度。
2. 以计算$x^{31}$ 为例，讨论如何设计计算格式才能有效地减少计算次数。

方案

问题1

• 手算得方程精确解为$\frac{100000001 \pm \sqrt{(1e9 + 1) ^ 2 - 4 * 1e9} }{2}$, 即$x_1 = 100000000, x2 = 1$
• 分别通过牛顿迭代法求解，看获得相同精度所需要的运算次数。

问题2

• 通过快速幂进行计算，快速幂的计算方法是将指数拆解成二进制，先计算出二的整数次幂，之后用二进制拼凑出整数。

代码

问题1

double eps, xnn;

const double xn1 = 1000000000.0, xn2 = 1.0;

double f(double x0)
{
	return x0 * x0  - (1000000001) * x0  + 1000000000;
}

double f1(double x0)
{
	return 2 * x0 - 100000001;
}

int diedai(double x0)
{
	int cnt = 0;
	while(abs(x0 - xn1) > eps && abs(x0 - xn2) > eps)
	{
		cnt++;
		x0 = x0 - f(x0) / f1(x0);
	}
	return cnt;
}

int main() {
//	freopen("output.out", "w", "stdout"); 	
	cin >> eps >> xnn; 
	cout << diedai(xnn) << "\n";
	return 0;
}

问题2

int cnt = 0;
double poww(double a, int b)
{
	double ans = 1.0, tmp = a;
	while(b)
	{
		if(b & 1) ans = ans * tmp;
		tmp = tmp * tmp;
		cnt ++;
		b >>= 1;
	}
	return ans;
}
int main() {
//	freopen("output.out", "w", "stdout"); 	
	double x, a;
	cin >> x >> a;  
	cout <<  poww(x, a) << " " << cnt << "\n";

	return 0;
}

算例

问题1

input1
0.00001 3
output1
52

问题2

input1
0.00001 3
output1
52

结果分析

• 结果和复杂度正确

第二章 非线性方程求根

问题

方案

问题1

对应三种递推式即可

代码

f1=@(x)(15-x^2)
f2=@(x)(15/(2*x+1))
f3=@(x)(x-(2*x^2+x-15)/(4*x+1))
x1=[2];x2=[2];x3=[2];
for i=2:100
    x1=[x1,f1(x1(i-1))]
    x2=[x2,f2(x2(i-1))]
    x3=[x3,f3(x3(i-1))]
end
subplot(3,1,1);
plot(x1);
axis([0,100,-10000,100])
subplot(3,1,2);
plot(x2);
axis([0,70,2,3])
subplot(3,1,3);
plot(x3);
axis([0,10,2,3])

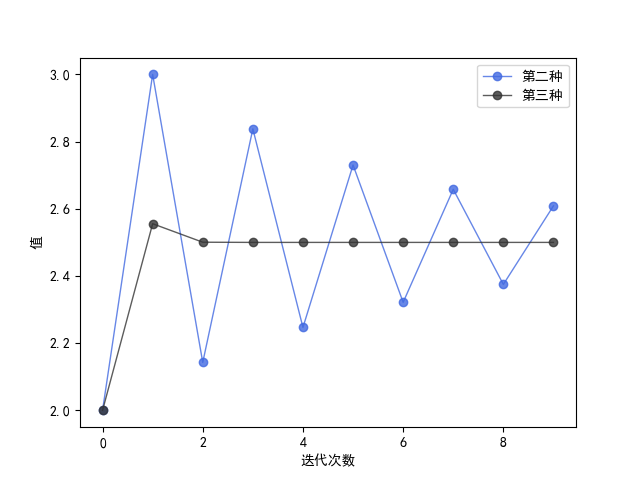
结果分析

$x_{k+1}=15-x_{k}^{2}$ 不收敛

后两个收敛速度如下

|

问题2

代码

f=@(x)(2-3*x-sin(x))
l=0;r=1;
fl=f(l);
cnt=0
while r-l>0.0005
    mid=l+(r-l)/2;
    fm=f(mid);
    cnt=cnt+1;
    if fl*fm>0
        l=mid;fl=fm;
    else
        r=mid
    end
end
fprintf('根为：%f,迭代次数为: %d\n',mid,cnt)

结果分析

迭代次数为11次

问题3

算法

使用牛顿迭代法：
$$
p_{n}=p_{n-1}-\frac{f\left(p_{n-1}\right)}{f^{\prime}\left(p_{n-1}\right)}, \quad n \geqslant 1
$$

代码

clc,clear;
syms x;
f1=1/2+1/4*x^2-x*sin(x)-1/2*cos(2*x);
df1=diff(f1);
f=matlabFunction(f1);
df=matlabFunction(df1);
x0=[pi/2,5*pi,10*pi];
cnt=[1,1,1];
tol=1e-5;
for i=1:3
    p0=x0(i);
    p=p0-f(p0)/df(p0);
    while cnt(i)<1000
        p=p0-f(p0)/df(p0);
        if abs(p-p0)<tol
            break
        end
        cnt(i)=cnt(i)+1;
        p0=p;
    end
    fprintf('p%d=%f,迭代次数：%d\n',i,p,cnt(i));
end

算例

初值为 $\frac{\pi}{2}, 5 \pi, 10 \pi$，迭代次数分别为15,19,249

结果分析

初值对牛顿迭代法有影响

问题4

算法

​二分法：$p_{n}=a_{n}+\frac{b_{n}-a_{n}}{2}$

​牛顿法：$p_{n}=p_{n-1}-\frac{f\left(p_{n-1}\right)}{f^{\prime}\left(p_{n-1}\right)}, \quad n \geqslant 1$

​割线法：$p_{n}=p_{n-1}-\frac{f\left(p_{n-1}\right)\left(p_{n-1}-p_{n-2}\right)}{f\left(p_{n-1}\right)-f\left(p_{n-2}\right)}$

​错位法：在割线法基础上，每次检验$p_{n}*p_{n-1}$的正负，来决定使用哪条割线来计算$p_{n+1}$

代码

syms x;
ff1=5*x-exp(x);
f=matlabFunction(ff1);
df1=diff(ff1);
df=matlabFunction(df1);
tol=1e-5;
cnt=[0,1,2,2];
%二分法
l=0;r=1;
fl=f(l);
while r-l>tol
    mid=l+(r-l)/2;
    fm=f(mid);
    cnt(1)=cnt(1)+1;
    if fl*fm>0
        l=mid;fl=fm;
    else
        r=mid
    end
end
fprintf('二分法根为：%.4f,迭代次数为: %d\n',mid,cnt(1))
%牛顿法
x0=0.5;
p0=x0;
p=p0-f(p0)/df(p0);
while cnt(2)<1000
    p=p0-f(p0)/df(p0);
    if abs(p-p0)<tol
        break
    end
    cnt(2)=cnt(2)+1;
    p0=p;
end
    fprintf('牛顿法根为：%.4f,迭代次数：%d\n',p,cnt(2));
%割线法
p0=0;
p1=1;
q0=f(p0);
q1=f(p1);
while cnt(3)<1000
    p=p1-q1*(p1-p0)/(q1-q0);
    if abs(p-p1)<tol
        break
    end
    cnt(3)=cnt(3)+1;
    p0=p1;
    q0=q1;
    p1=p;
    q1=f(p);
end
fprintf('割线法根为：%.4f,迭代次数：%d\n',p,cnt(3));
%错位法
p0=0;
p1=1;
q0=f(p0);
q1=f(p1);
while cnt(4)<1000
    p=p1-q1*(p1-p0)/(q1-q0);
    if abs(p-p1)<tol
        break
    end
    cnt(4)=cnt(4)+1;
    q=f(p);
    if q*q1<0
        p0=p1;q0=q1;
    else
        p1=p;q1=q;
    end
end
fprintf('错位法根为：%.4f,迭代次数：%d\n',p,cnt(4));

结果分析

	根	迭代次数
二分法	0.2592	17
牛顿法	0.2592	4
割线法	0.2592	6
错位法	0.2592	6

第三章 插值多项式

实验

问题1

代码

clc,clear;
x1=0:pi/11:pi;
x2=0:pi/21:pi;
y1=sin(x1);
y2=sin(x2);
pp=csape(x1,y1,'variational');
yy=ppval(pp,x1);
subplot(2,2,1);
hold on;
plot(x1,yy);
scatter(x1,yy);
title('自然边界');
pp=csape(x2,y2,'variational');
yy=ppval(pp,x2);
subplot(2,2,2);
hold on;
plot(x2,yy);
scatter(x2,yy);
title('自然边界');
pp=csape(x1,y1,'clamped');
yy=ppval(pp,x1);
subplot(2,2,3);
hold on;plot(x1,yy);
scatter(x1,yy);
title('固定边界');
pp=csape(x2,y2,'clamped');
yy=ppval(pp,x2);
subplot(2,2,4);
hold on;
plot(x2,yy);
scatter(x2,yy);
title('固定边界');
figure;
pp=csape(x1,y1,'periodic');
yy=ppval(pp,x1);
subplot(2,2,1);
hold on;
plot(x1,yy);
scatter(x1,yy);
title('周期边界');
pp=csape(x2,y2,'periodic');
yy=ppval(pp,x2);
subplot(2,2,2);
hold on;
plot(x2,yy);
scatter(x2,yy);
title('周期边界');
pp=csape(x1,y1,'not-a-knot');
yy=ppval(pp,x1);
subplot(2,2,3);
hold on;
plot(x1,yy);
scatter(x1,yy);
title('非扭结边界');
pp=csape(x2,y2,'not-a-knot');
yy=ppval(pp,x2);
subplot(2,2,4);
hold on;
plot(x2,yy);
scatter(x2,yy);
title('非扭结边界');

算例

### 结果分析

21个点的拟合结果要比11个点的要好

第四章 数值微分和数值积分

算法

实验

问题3

方案

定理 设 $f \in C^{4}[a, b], n$ 是偶数, $h=(b-a) / n, x_{j}=a+j h(j=0,1, \cdots, n)$ 。存在一 个 $\mu \in(a, b)$ 使得对于 $n$ 个子区间的复合 Simpson 法郧及其误差项可以写为

$$
\int_{a}^{b} f(x) \mathrm{d} x=\frac{h}{2}\left[f(a)+2 \sum_{i=1}^{n-1} f\left(x_{j}\right)+f(b)\right]-\frac{b-a}{12} h^{2} f^{\prime \prime}(\mu)
$$
可得1
$$
\int_{a}^{b} f(x) \mathrm{d} x=\frac{h}{3}\left[f(a)+2 \sum_{i=1}^{(n / 2)-1} f\left(x_{2 j}\right)+4 \sum_{1}^{n / 2} f\left(x_{2,-1}\right)+f(b)\right]-\frac{b-a}{180} h^{4} f^{(4)}(\mu)
$$

代码

function s=trapezoidal(f,a,b,n)
h=(b-a)/n;
sum=0;
for i=1:n-1
    sum=sum+feval(f,a+h*i);
end
s=h/2*(feval(f,a)+feval(f,b)+2*sum);
end

clc,clear;format long;syms x;
f =@(x) exp(-x^2/2)/sqrt(2*pi);
ans=int(f,x,0,1);
ans=double(ans);
fprintf('精确解为%.12f\n',ans);
ans1=trapezoidal(f,0,1,100);
fprintf('复合梯形公式解为%.12f,误差为%.12f\n',ans1,abs(ans-ans1));
ans2=simpson(f,0,1,100);
fprintf('simpson解为%.12f,误差为%.12f\n',ans2,abs(ans-ans2));

结果分析

复合梯形公式误差0.000002016429， Simpson公式误差0.000000000027
Simpson方法误差较小。

问题4

代码

clc,clear;format long;syms x;
f =@(x) (2+sin(2*sqrt(x)));
n=[10,20,40];
for i=1:3
    fprintf("h=%f时，复合梯形公式结果为%.12f\n",5/n(i),trapezoidal(f,1,6,n(i)));
    fprintf("h=%f时，Simpson公式结果为%.12f\n\n",5/n(i),simpson(f,1,6,n(i)));
end

结果分析

h	0.5	0.25	0.125
复合梯形公式	8.193854565173	8.186049263770	8.184120191790
Simpson	8.183015494056	8.183447496636	8.183477167797

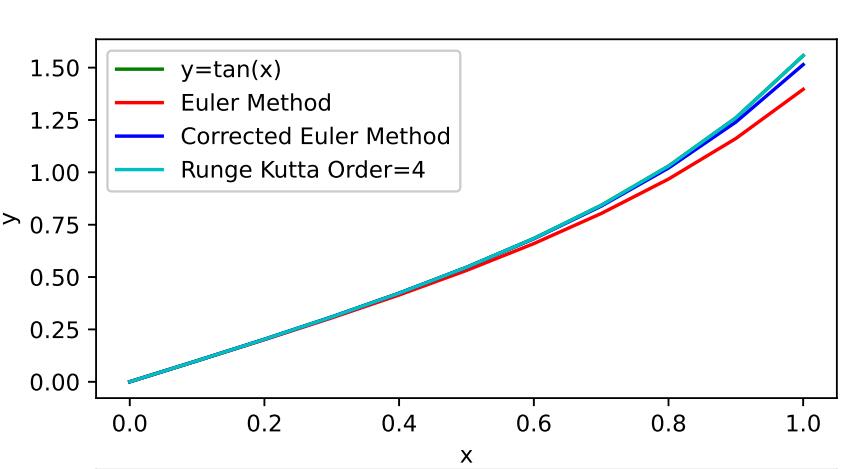
第五章 常微分方程数值解

实验

问题

方案

欧拉法：
$$
w_{i+1}=w_{i}+h f\left(t_{i}, w_{i}\right), \quad i=0,1, \cdots, N-1
$$

梯形预估修正格式：
$$
w_{i+1}=w_{i}+\frac{h}{2}\left[f\left(t_{i}, w_{i}\right)+f\left(t_{i+1}, w_{i}+h f\left(t_{i}, w_{i}\right)\right)\right], \quad i=0,1,2, \cdots, N-1
$$

4阶龙格库塔格式：
$$
\begin{aligned}
&w_{0}=\alpha \
&k_{1}=h f\left(t_{i}, w_{i}\right)\
&k_{2}=h f\left(t_{i}+\frac{h}{2}, w_{i}+\frac{1}{2} k_{1}\right) \
&k_{3}=h f\left(t_{i}+\frac{h}{2}, w_{i}+\frac{1}{2} k_{2}\right) \
&k_{4}=h f\left(t_{i+1}, w_{i}+k_{3}\right) \
&w_{i+1}=w_{i}+\frac{1}{6}\left(k_{1}+2 k_{2}+2 k_{3}+k_{4}\right)
\end{aligned}
$$

代码

function E=euler1(f,a,b,y0,n)
h=(b-a)/n;
Y(1)=y0;
T=a:h:b;
for i=1:n
    Y(i+1)=Y(i)+h*feval(f,0,Y(i));
end
E=[T',Y'];
end

function E=trape(f,a,b,y0,n)
h=(b-a)/n;
Y(1)=y0;
T=a:h:b;
for i=1:n
    Y(i+1)=Y(i)+h/2*(feval(f,0,Y(i))+feval(f,0,Y(i)+h*feval(f,0,Y(i))));
end
E=[T',Y'];
end


function E=rk4(f,a,b,y0,n)
h=(b-a)/n;
Y(1)=y0;
T=a:h:b;
for i=1:n
    k1=h*feval(f,0,Y(i));
    k2=h*feval(f,0+h/2,Y(i)+k1/2);
    k3=h*feval(f,0+h/2,Y(i)+k2/2);
    k4=h*feval(f,0+h,Y(i)+k3);
    Y(i+1)=Y(i)+(k1+2*k2+2*k3+k4)/6;
end
E=[T',Y'];
end

clc,clear;syms y;
f=@(t,y)1+y^2;
y0=0;a=0;b=1.5;
[X,Y]=ode45(f,[a,b],y0);
subplot(2,2,1);
plot(X,Y);
title('y=tan(x)');
E=euler1(f,a,b,y0,50);
subplot(2,2,2);
plot(E(:,1),E(:,2));
title('Euler Method');
E=trape(f,a,b,y0,50);
subplot(2,2,3);
plot(E(:,1),E(:,2));
title('Corrected Euler Method');
E=rk4(f,a,b,y0,50);
subplot(2,2,4);
plot(E(:,1),E(:,2));
title('Runge Kutta Order=4');

figure;[X,Y]=ode45(f,[a,b],y0);
E1=euler1(f,a,b,y0,50);
E2=trape(f,a,b,y0,50);
E3=rk4(f,a,b,y0,50);
plot(X,Y,'k',E1(:,1),E1(:,2),'r',E2(:,1),E2(:,2),'gs',E3(:,1),E3(:,2),'b');
legend('y=tan(x)','Euler Method','Corrected Euler Method','Runge Kutta Order=4');

算例

结果分析

Runge Kutta Order=4 优于修正梯形公式优于欧拉方法

问题4

方案

将原方程转化为
$$
\frac{d\left(y^{\prime}\right)}{d t}=\mu\left(1-\left(\int_{0}^{t} y^{\prime}(x) d x+1\right)^{2}\right) y^{\prime}-\left(\int_{0}^{t} y^{\prime}(x) d x+1\right)
$$

解出即可

clc,clear;
f=@(t,y) (t-y)/2;
a=0;b=3;
n=[3,6,12,24];
[X1,Y1]=ode45(f,[a,b],1);
fprintf('精确解：%.12f\n',Y1(end));
for cnt=1:4
    h=(b-a)/n(cnt);
    t=a;
    Y(1)=1;
    X=a:h:b;
    X=X';
    for i=1:3
        k1=h*feval(f,t,Y(i));
        k2=h*feval(f,t+h/2,Y(i)+k1/2);
        k3=h*feval(f,t+h/2,Y(i)+k2/2);
        k4=h*feval(f,t+h,Y(i)+k3);
        Y(i+1)=Y(i)+(k1+2*k2+2*k3+k4)/6;t=a+i*h;
    end
    for i=4:n(cnt)
        t=a+i*h;
        Y(i+1)=Y(i)+h*(55*f(t-h,Y(i))-59*f(t-2*h,Y(i-1))+37*f(t-3*h,Y(i-2))-9*f(t-4*h,Y(i-3)))/24;
        Y(i+1)=Y(i)+h*(9*f(t,Y(i+1))+19*f(t-h,Y(i))-5*f(t-2*h,Y(i-1))+f(t-3*h,Y(i-2)))/24;
    end
    subplot(2,2,cnt);
    plot(X,Y');
    title(num2str(h));
    fprintf('h=%f时，数值解为%.12f,误差为%.12f\n',h,Y(n(cnt)+1),abs(Y1(end)-Y(n(cnt)+1)));
end

结果分析

h	数值解	误差
1	1.670185989804	0.000795482163
0.5	1.669234936809	0.000155570832
0.25	1.669381576972	0.000008930669
0.125	1.669389992781	0.000000514860

h越小，误差越小。

第六、七章 线性方程组求解

实验

问题

LU分解算法

设 $\mathbf{A}=\left(a_{i, j}\right){n \times n}$, 分解为 $\mathbf{A}=\mathbf{L U}$ 的形式, 其中 $\mathbf{L}$ 为对角元为 1 的下三角矩阵, $\mathbf{U}$ 为上三角矩阵, 即
$$
\left(\begin{array}{cccc}
a{11} & a_{12} & \cdots & a_{1 n} \
a_{21} & a_{22} & \cdots & a_{2 n} \
\vdots & \vdots & \ddots & \vdots \
a_{n 1} & a_{n 2} & \cdots & a_{n n}
\end{array}\right)=\left(\begin{array}{cccc}
1 & 0 & \cdots & 0 \
l_{21} & 1 & \cdots & 0 \
\vdots & \vdots & \ddots & \vdots \
l_{n 1} & l_{n 2} & \cdots & 1
\end{array}\right)\left(\begin{array}{cccc}
u_{11} & u_{12} & \cdots & u_{1 n} \
0 & u_{22} & \cdots & u_{2 n} \
\vdots & \vdots & \ddots & \vdots \
0 & 0 & \cdots & u_{n n}
\end{array}\right)
$$
按照矩阵乘法规则, 比较系数, 可得
$$
\left{\begin{array}{lr}
u_{1 j}=a_{1 j} & (j=1,2, \cdots, n) \
l_{i 1}=\frac{a_{i 1}}{u_{11}} & (i=2,3, \cdots, n) \
u_{i j}=a_{i j}-\sum_{k=1}^{i-1} l_{i k} u_{k j} & (i=2, \cdots, n, j=i, \cdots, n) \
l_{i j}=\left(a_{i j}-\sum_{k=1}^{j-1} l_{i k} u_{k j}\right)
\end{array} \quad(j=1,2, \cdots, n, i=j+1, \cdots, n)\right.
$$

代码

function[L,U,X]=lu(A,B,n)
for i=1:n
    L(i,i)=1;
end
for i=1:n
    U(1,i)=A(1,i)/L(1,1);
    L(i,1)=A(i,1)/U(1,1);
end
for i=2:n-1
    zc=0;
    for j=1:i-1
        zc=zc+L(i,j)*U(j,i);
    end
    U(i,i)=A(i,i)-zc;
    for j=i+1:n
        U(i,j)=A(i,j);
        L(j,i)=A(j,i);
        for k=1:i-1
            U(i,j)=U(i,j)-L(i,k)*U(k,j);L(j,i)=L(j,i)-L(j,k)*U(k,i);
        end
        L(j,i)=L(j,i)/U(i,i);
    end
end
U(n,n)=A(n,n);
for i=1:n-1
    U(n,n)=U(n,n)-L(n,i)*U(i,n);
end
Y(1)=B(1);
for i=2:n
    Y(i)=B(i);
    for j=1:i-1
        Y(i)=Y(i)-L(i,j)*Y(j);
    end
end
X(n)=Y(n)/U(n,n);
for i=n-1:-1:1
    X(i)=Y(i);
    for j=i+1:n
        X(i)=X(i)-U(i,j)*X(j);
    end
    X(i)=X(i)/U(i,i);
end
end
clc,clear;format short;
A=[4 -1 1;4 -8 1;-2 1 5];
B=[7;-21;15];
[L,U,X]=lu(A,B,3);
disp(L);
disp(U);
disp(X);

Jacobi方法

Jacobi 迭代法包含了从 $\boldsymbol{A x}=\boldsymbol{b}$ 中的第 $i$ 个方程求解第 $i$ 个分量 $x_{i}$, 得到(假设 $a_{i u} \neq 0$ )
$$
x_{i}=\sum_{\substack{j=1 \ j \neq i}}^{n}\left(-\frac{a_{i} x_{j}}{a_{i i}}\right)+\frac{b_{i}}{a_{i i}}, \quad i=1,2, \cdots, n
$$
以及当 $k \geqslant 1$ 时, 从分量 $\boldsymbol{x}^{(k-1)}$ 计算生成各个 $\boldsymbol{x}{i}^{(k)}$
$$
x{i}^{(k)}=\frac{\sum_{\substack{j=1 \ j \neq i}}^{n}\left(-a_{i j} x_{j}^{(k-1)}\right)+b_{i}}{a_{i i}}, i=1,2, \cdots, n
$$

代码

function [cnt,X]=Jacobi(A,B,XO,tol)
n=length(B);
cnt=1;
X=zeros(n,1);
while cnt<=1000
    for i=1:n
        X(i)=(B(i)-A(i,[1:i-1,i+1:n])*XO([1:i-1,i+1:n]))/A(i,i);
    end
    err=abs(norm(X-XO));
    XO=X;
    if(err<tol)
        break
    end
    cnt=cnt+1;
end
end

Gauss_Seidel方法

考虑改进上面的算法。 $x^{(k-1)}$ 的分量可以用来计算 $x_{i}^{(k)}$ 。因为对 $i>1$, $x_{1}^{(k)}, \cdots, x_{i-1}^{(k)}$ 已经计算出来了, 并且可能比 $x_{1}^{(k-1)}, \cdots, x_{i-1}^{(k-1)}$ 更接近于实际解 $x_{1}, \cdots, x_{i-1}$, 显然使用那些新近计算出来的值来计算 $x_{i}^{(k)}$ 更合理。也就是说, 可以使用
$$
x_{i}^{(k)}=\frac{-\sum_{j=1}^{i=1}\left(a_{i j} x_{j}^{(k)}\right)-\sum_{i=i+1}^{n}\left(a_{i j} x_{j}^{(k-1)}\right)+b_{i}}{a_{i i}}, i=1,2, \cdots, n
$$
来代替方程。这种改进称作 Gauss-Seidel 迭代法。

代码

function [cnt,X]=Gauss_Seidel(A,B,XO,tol)
n=length(B);
cnt=1;
X=zeros(n,1);
while cnt<1000
    for i=1:n
        if i==1
            X(1) = (B(1)-A(1,2:n)*XO(2:n))/A(1,1);
        elseif i==n 
            X(n) = (B(n)-A(n,1:n-1)*X(1:n-1))/A(n,n);
        else
            X(i) = (B(i)-A(i,1:i-1)*X(1:i-1)-A(i,i+1:n)*XO(i+1:n))/A(i,i);
        end
    end
    err=abs(norm(X-XO));XO=X;
    if(err<tol)
        break
    end
    cnt=cnt+1;
end
end
clc,clear;format long;
A=[4 -1 1;4 -8 1;-2 1 5];
B=[7;-21;15];XO=[0;0;0];
[k,X]=Jacobi(A,B,XO,1e-6);
disp('Jacobi');
disp(k);disp(X);
[k,X]=Gauss_Seidel(A,B,XO,1e-6);
disp('Gauss_Seidel');
disp(k);disp(X);

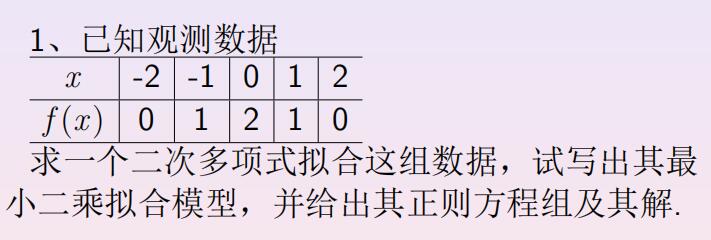
第八章 曲线拟合与函数逼近

算法

实验

问题

方案

问题1

设 $\left(x_{k}, y_{k}\right){k=1}^{N}$ 为N个初始点。对于最小二乘二次多项式方程的系数表示为:
$$
y=f(x)=A x^{2}+B x+C
$$
其正则线性方程组为:
$$
\left{\begin{array}{l}
\left(\sum{k=1}^{N} x_{k}^{4}\right) A+\left(\sum_{k=1}^{N} x_{k}^{3}\right) B+\left(\sum_{k=1}^{N} x_{k}^{2}\right) C=\sum_{k=1}^{N} y_{k} x_{k}^{2} \
\left(\sum_{k=1}^{N} x_{k}^{3}\right) A+\left(\sum_{k=1}^{N} x_{k}^{2}\right) B+\left(\sum_{k=1}^{N} x_{k}\right) C=\sum_{k=1}^{N} y_{k} x_{k} \
\left(\sum_{k=1}^{N} x_{k}^{2}\right) A+\left(\sum_{k=1}^{N} x_{k}\right) B+N C=\sum_{k=1}^{N} y_{k}
\end{array}\right.
$$
代入数据：
$$
\left{\begin{array}{l}
34 A+10C=2\
10B=0 \
10A+5C=4
\end{array}\right.
$$
解得
$$
\left{\begin{array}{l}
\mathrm{A}=-0.4286 \
\mathrm{~B}=0 \
\mathrm{C}=1.6571
\end{array}\right.
$$
故求得最小二乘拟合方程为: $y=-0.4286 x^{2}+1.6571$

问题2

可以将$y=ae^{-bx}$ 转化为$lny = lna - bx$, 然后线性去做类似上面

得到$y = 1.8123e^{0.3699x}$

第九章 特征值和特征向量

实验

问题

方案

幂法

function [u,X]=mi(n,A,X,tol)
cnt=1;u=0;
while cnt<1000
    Y=A*X;u1=max(Y);
    err=X-Y./u1;
    X=Y./u1;
    u=u1;
    if(abs(u1-u)<tol&&norm(err)<tol)
        break
    end
    cnt=cnt+1;
end
end

对称幂法

function[u,X]=dui(n,A,X,tol)
cnt=1;
X=X./sqrt(X'*X);
while cnt<1000
    Y=A*X;
    u=X'*Y;
    if sqrt(Y'*Y)==0
        break;
    end
    err=sqrt((X-Y./sqrt(Y'*Y))'*(X-Y./sqrt(Y'*Y)));X=Y./sqrt(Y'*Y);
    if err<tol
        break
    end
    cnt=cnt+1;
end
end

反幂法

function[u,X]=fan(n,A,X,tol,u1)
cnt=1;
[m,n]=size(X);
Y=zeros(m,n);I=eye(m);
H=A-u1.*I;[L,U]=lu(H);
while cnt<1000
    p=max(X);
    Y=X./p;
    Z=L\Y;
    X=U\Z;
    p=max(X);
    u=u1+1/p;
    if abs(1/p-1/uu)<tol
        break
    end
    cnt=cnt+1;
    uu=p;
end
end

结果分析

幂法和对称幂法都找到了最大的特征值 𝜆 = 6然后对应的特
征向量都形如$\alpha(1,-1,1)^{T}$